Geometric Optimisation Via Spectral Shifting
Roman Poya, Rogelio Ortigosa , Theodore Kim
ACM Transactions on Graphics, Vol 42, No 3, Article No 29, pp 1-15 (presented at SIGGRAPH 2023)
Awarded the Siemens Author Award (April 2024)

Abstract
We present a geometric optimisation framework that can recover fold-over free maps from non-injective initial states using popular flip-preventing distortion energies. Since flip-preventing energies are infinite for folded configurations, we propose a new regularisation scheme that shifts the singular values of the deformation gradient. This allow us to re-use many existing algorithms, especially locally injective methods for initially folded maps. Our regularisation is suitable for both singular value- and invariant-based formulations, and systematically contributes multiple stabilisers to the Hessian. In contrast to proxy-based techniques, we maintain second-order convergence. Compact expressions for the energy eigensystems can be obtained for our extended stretch invariants, enabling the use of fast projected Newton solvers. Although spectral shifting in general has no theoretical guarantees that the global minimum is an injection, extensive experiments show that our framework is fast and extremely robust in practice, and capable of generating high-quality maps from severely distorted, degenerate and folded initialisations.
Synopsis
Distortion energies are typically expressed in terms of a set of deformation invariants such as Cauchy-Green [Bonet & Wood 2016a], polyconvex [Bonet 2016b], stretch tensor [B. Smith 2019] or singular values [Xu et. al. 2015] of the deformation gradient tensor  . The deformation gradient (more commonly known as the Jacobian of mapping although in our case we reserve the word Jacobian for the determinant of
. The deformation gradient (more commonly known as the Jacobian of mapping although in our case we reserve the word Jacobian for the determinant of  ) admits the following Signed Singular Value Decomposition (SSVD) [Irving 2004]
) admits the following Signed Singular Value Decomposition (SSVD) [Irving 2004]
 . The deformation gradient (more commonly known as the Jacobian of mapping although in our case we reserve the word Jacobian for the determinant of
. The deformation gradient (more commonly known as the Jacobian of mapping although in our case we reserve the word Jacobian for the determinant of  ) admits the following Signed Singular Value Decomposition (SSVD) [Irving 2004]
) admits the following Signed Singular Value Decomposition (SSVD) [Irving 2004]

where  is the diagonal matrix of singular-values
is the diagonal matrix of singular-values  . Restricting ourselves to 2-dimensions (for the sake of this presentation) we express the desired distortion energy either in terms of stretch tensor invariants or signular values as follows
. Restricting ourselves to 2-dimensions (for the sake of this presentation) we express the desired distortion energy either in terms of stretch tensor invariants or signular values as follows
 is the diagonal matrix of singular-values
is the diagonal matrix of singular-values  . Restricting ourselves to 2-dimensions (for the sake of this presentation) we express the desired distortion energy either in terms of stretch tensor invariants or signular values as follows
. Restricting ourselves to 2-dimensions (for the sake of this presentation) we express the desired distortion energy either in terms of stretch tensor invariants or signular values as follows

where  ,
,  and,
and,  are the stretch tensor invariants [B. Smith 2019] which help abstract the math. Consider the Symmetric Dirichlet (SD) energy [Smith & Schaefer 2015] in 2-dimensions now which can be expressed in either of these formats as
are the stretch tensor invariants [B. Smith 2019] which help abstract the math. Consider the Symmetric Dirichlet (SD) energy [Smith & Schaefer 2015] in 2-dimensions now which can be expressed in either of these formats as
 ,
,  and,
and,  are the stretch tensor invariants [B. Smith 2019] which help abstract the math. Consider the Symmetric Dirichlet (SD) energy [Smith & Schaefer 2015] in 2-dimensions now which can be expressed in either of these formats as
are the stretch tensor invariants [B. Smith 2019] which help abstract the math. Consider the Symmetric Dirichlet (SD) energy [Smith & Schaefer 2015] in 2-dimensions now which can be expressed in either of these formats as

Following [B. Smith 2019] and [Poya 2023], the four Hessian eigenvalues for this energy can be found analytically and written concisely as

It is evident that, given that no triangles are flipped in the discrete setting (i.e. all singular-values are positive), the above Hessian always has three positive eigenvalues. The last eigenvalue can be negative and hence, the SD energy can turn indefinite during the course of deformation.
Proposed Idea
While many strategies exist for convexifying an energy, the idea we propose is, intuitively, to spectrally shift the singular values of the deformation gradient tensor as follows

where  is a scaled identity matrix acting as a regulariser and
is a scaled identity matrix acting as a regulariser and  is the regularisation parameter. More specifically, every singular-value
is the regularisation parameter. More specifically, every singular-value  is shifted by an amount
is shifted by an amount  to
to  , isotropically. Instead of working with
, isotropically. Instead of working with  we can simply choose to work with
we can simply choose to work with  by plugging it into any desired distortion energy and in return obtaining a regularised distortion energy. For instance, the Regularised Symmetric Dirichlet (RSD) energy then looks like this
by plugging it into any desired distortion energy and in return obtaining a regularised distortion energy. For instance, the Regularised Symmetric Dirichlet (RSD) energy then looks like this
 is a scaled identity matrix acting as a regulariser and
is a scaled identity matrix acting as a regulariser and  is the regularisation parameter. More specifically, every singular-value
is the regularisation parameter. More specifically, every singular-value  is shifted by an amount
is shifted by an amount  to
to  , isotropically. Instead of working with
, isotropically. Instead of working with  we can simply choose to work with
we can simply choose to work with  by plugging it into any desired distortion energy and in return obtaining a regularised distortion energy. For instance, the Regularised Symmetric Dirichlet (RSD) energy then looks like this
by plugging it into any desired distortion energy and in return obtaining a regularised distortion energy. For instance, the Regularised Symmetric Dirichlet (RSD) energy then looks like this

The four eigenvalues of RSD are then obtained in a similar fashion

An interesting property of this regularisation is that, the regularised energy has a similar eigenstructure to that of the original one with the addition of the stabiliser (in the last eigenvalue - accidentally the troublesome eigenvalue). This is due to the fact that, spectral shifting is a linear transform and preserves the convex (non-convex) nature of the energy and only shifts the bounds of convexity. In fact, we can show that for a large positive constant value of  the RSD energy is a "convexified" version of SD.
the RSD energy is a "convexified" version of SD.
 the RSD energy is a "convexified" version of SD.
the RSD energy is a "convexified" version of SD.
The question then is: why do this instead of clamping the eigenvalues of original SD energy to zero (in fact, we even have them in closed-form)? Well, clamping the eigenvalues of original SD deteriorates the convergence of a second order solver such as the quadratic convergence of Newton while spectral shifting results in a new (potentially convex) energy that retains the theoretically guaranteed convergence of nonlinear solvers.
Recovering Injectivity
While this regularisation technique can make energies convex and easy to optimise using convex minimisation approaches, intuitively, it drops their flip-preventing (locally-injective-preserving) nature as evident in the energy and Hessian eigenvalues of RSD. However, it opens another avenue and that is recovering flip-free configuration using flip-preventing energies. This is a natural extension of spectral shifting and novel to our contribution. The idea is, if we have a target mesh with flipped elements, we would start with a large enough  such that it turns the lowest signular-value of the deformation gradient over all the elements to non-negative and then we progressively decrease
such that it turns the lowest signular-value of the deformation gradient over all the elements to non-negative and then we progressively decrease  by running Newton minimisation multiple times each time with a new
by running Newton minimisation multiple times each time with a new  . In the beginning of the optimisation we also often enjoy the benefit of quadratic convergence of Newton but as
. In the beginning of the optimisation we also often enjoy the benefit of quadratic convergence of Newton but as  is decreased sufficiently we resort to clamping the eigenvalues. There are many formulae that we tested for the decay of
is decreased sufficiently we resort to clamping the eigenvalues. There are many formulae that we tested for the decay of  over the course of optimisation including considering
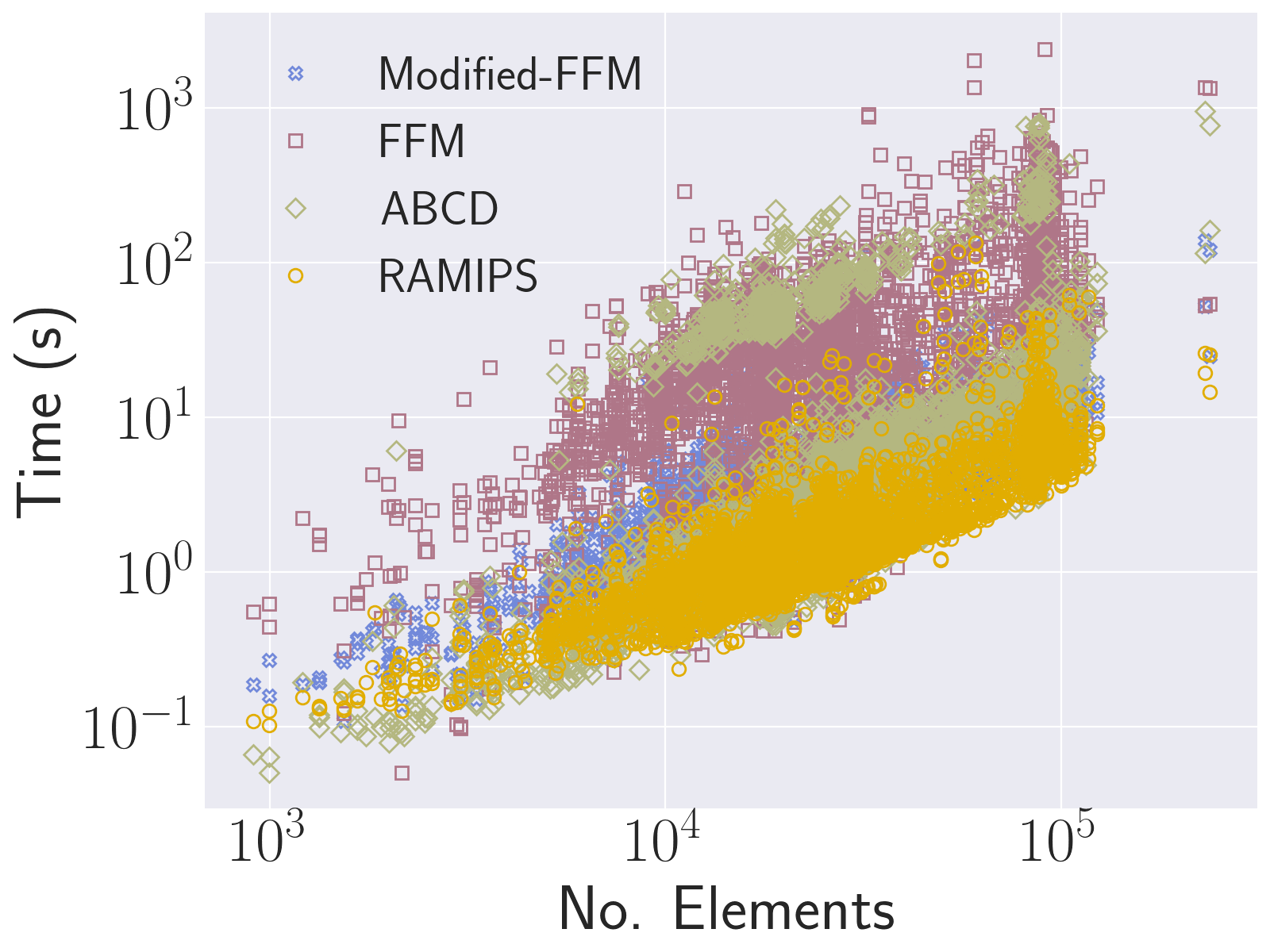
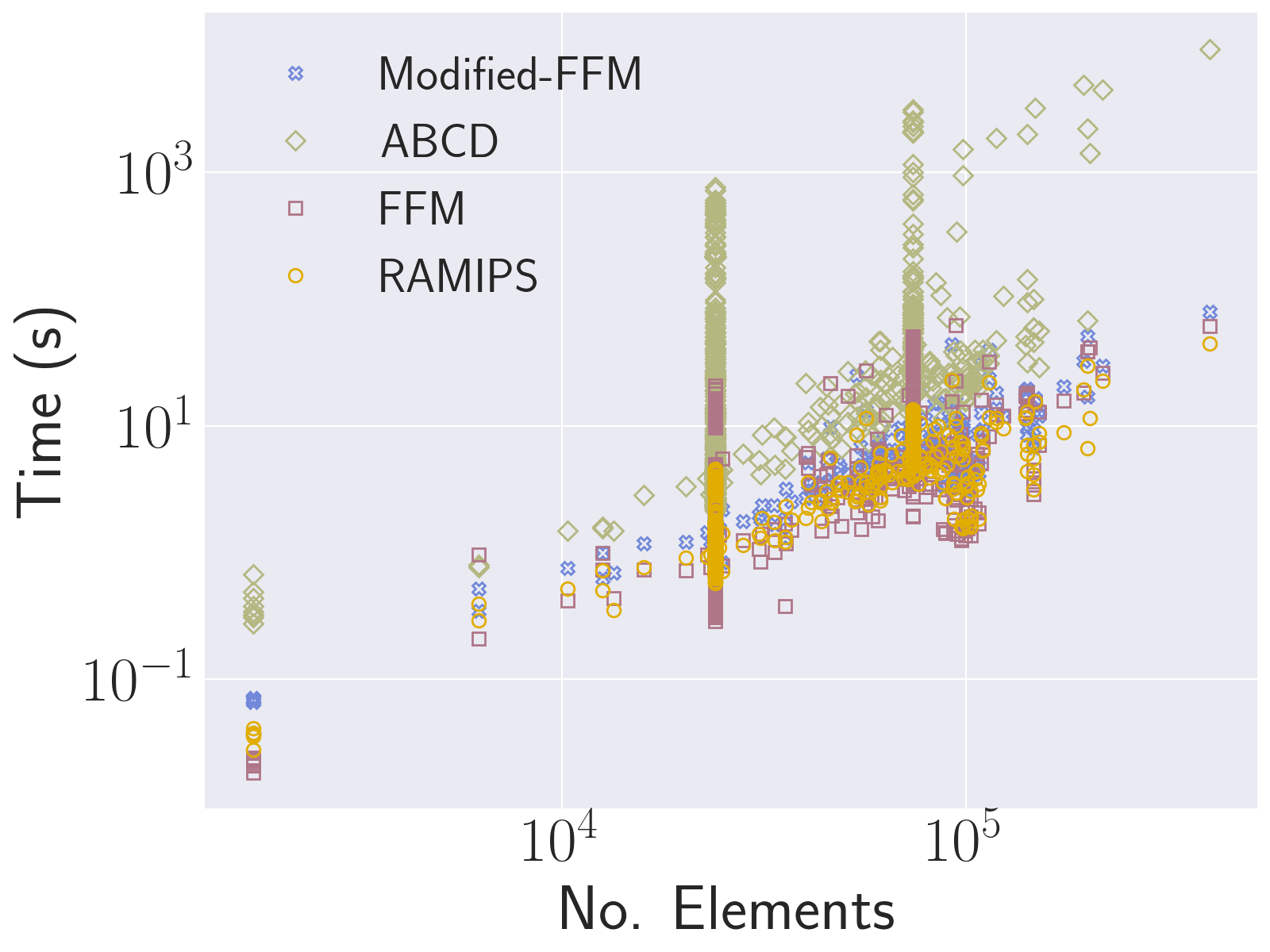
over the course of optimisation including considering  to vary from element to element (i.e. considering it as a variable and carrying out energy derivatives, respectively). Our extensive evaluation has revealed that despite being a "best-effort" approach, this technique results in a fast and extremely robust framework for recovering flip-free configurations, successfully passing large-scale local injectivity benchmarks and outperforming state-of-the-art techniques by orders of magnitude.
to vary from element to element (i.e. considering it as a variable and carrying out energy derivatives, respectively). Our extensive evaluation has revealed that despite being a "best-effort" approach, this technique results in a fast and extremely robust framework for recovering flip-free configurations, successfully passing large-scale local injectivity benchmarks and outperforming state-of-the-art techniques by orders of magnitude.
 such that it turns the lowest signular-value of the deformation gradient over all the elements to non-negative and then we progressively decrease
such that it turns the lowest signular-value of the deformation gradient over all the elements to non-negative and then we progressively decrease  by running Newton minimisation multiple times each time with a new
by running Newton minimisation multiple times each time with a new  . In the beginning of the optimisation we also often enjoy the benefit of quadratic convergence of Newton but as
. In the beginning of the optimisation we also often enjoy the benefit of quadratic convergence of Newton but as  is decreased sufficiently we resort to clamping the eigenvalues. There are many formulae that we tested for the decay of
is decreased sufficiently we resort to clamping the eigenvalues. There are many formulae that we tested for the decay of  over the course of optimisation including considering
over the course of optimisation including considering  to vary from element to element (i.e. considering it as a variable and carrying out energy derivatives, respectively). Our extensive evaluation has revealed that despite being a "best-effort" approach, this technique results in a fast and extremely robust framework for recovering flip-free configurations, successfully passing large-scale local injectivity benchmarks and outperforming state-of-the-art techniques by orders of magnitude.
to vary from element to element (i.e. considering it as a variable and carrying out energy derivatives, respectively). Our extensive evaluation has revealed that despite being a "best-effort" approach, this technique results in a fast and extremely robust framework for recovering flip-free configurations, successfully passing large-scale local injectivity benchmarks and outperforming state-of-the-art techniques by orders of magnitude.